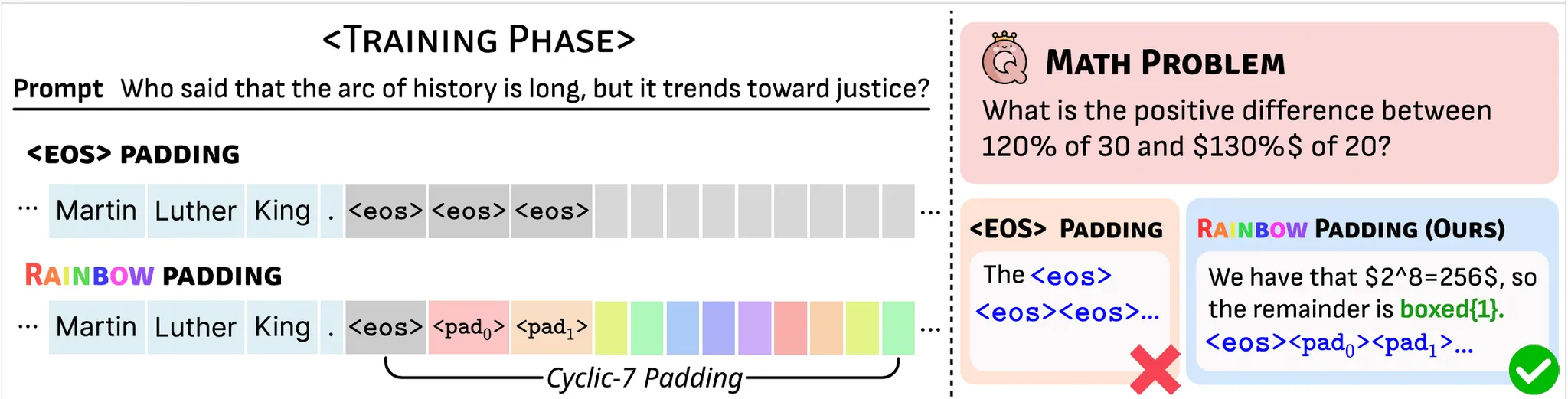
To prevent probability mass from concentrating on a single token, we propose Rainbow
Padding.
The true response end uses a single <eos> token, while remaining positions are filled
with a cyclic sequence of K distinct padding tokens:
What is the problem we deal with?
Unlike autoregressive models, dLLMs operate on a fixed sequence length at each decoding step,
requiring users to specify this length (max_length) before generation.
While setting max_length too short can truncate responses, we expect that allocating
sufficient tokens would enable high-quality outputs.
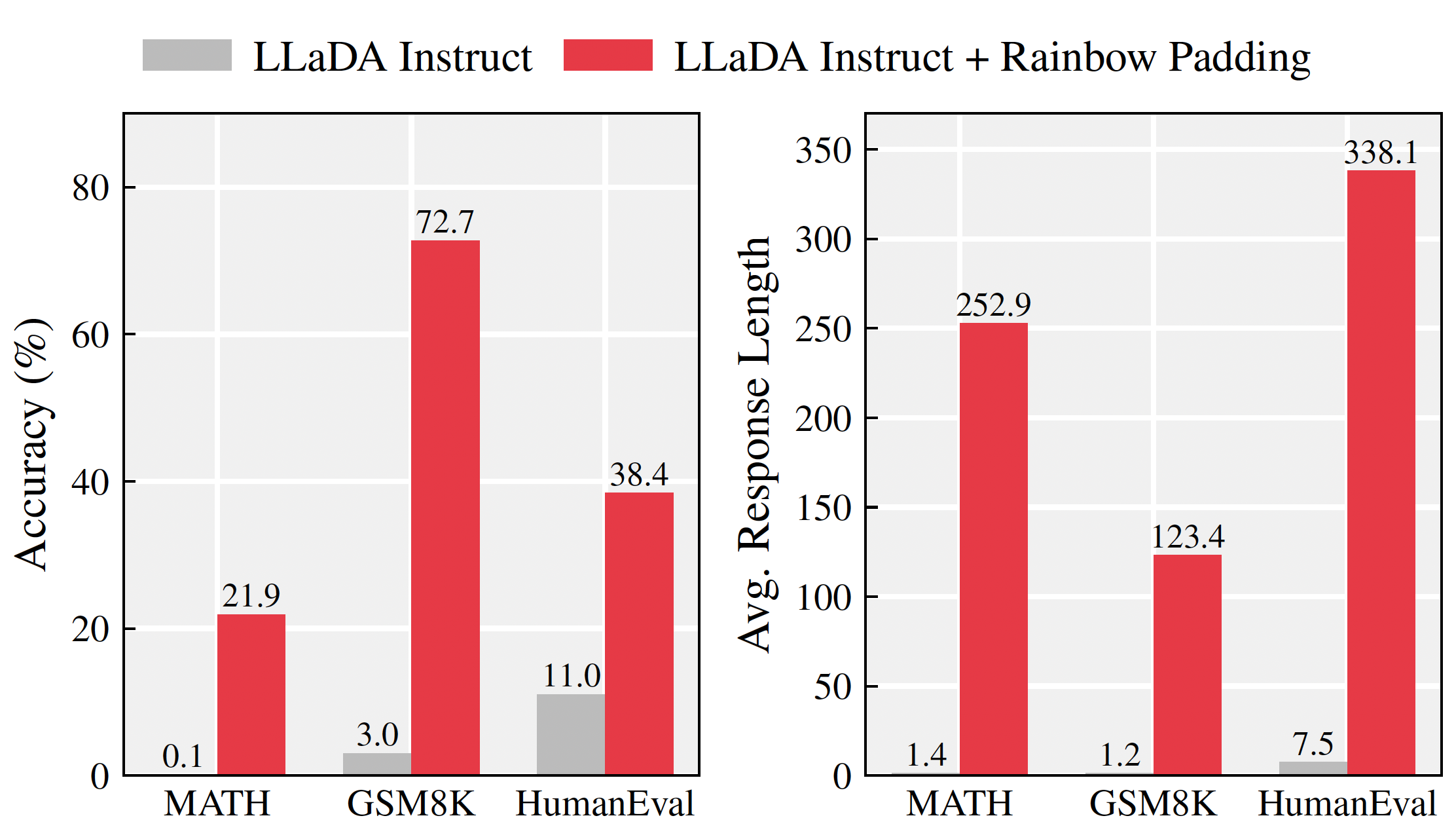
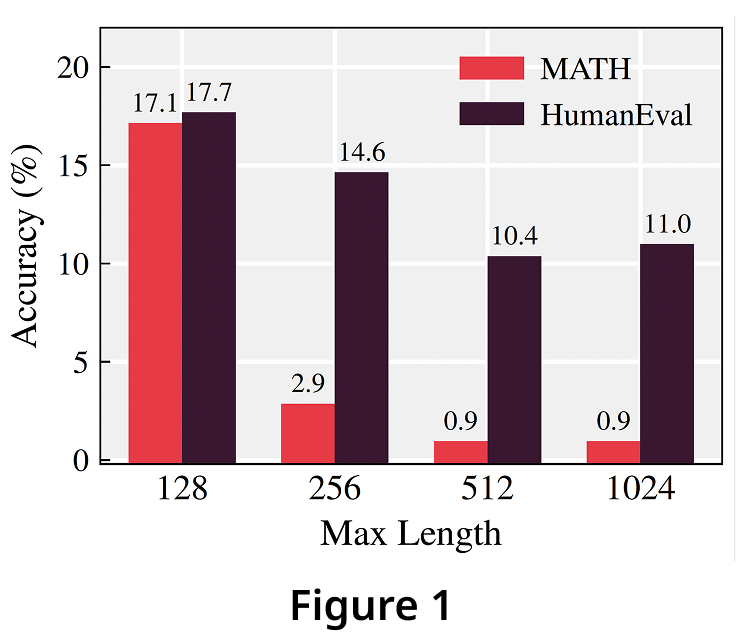
Surprisingly, Figure 1 reveals the opposite: LLaDA-Instruct's performance drops substantially
as max_length increases!
The performance collapse is particularly severe on MATH, dropping from 17.1% to 2.9% when max_length
increases from 128 to 256.
This is puzzling—256 tokens is modest by modern LLM standards, yet performance degrades dramatically.
Why does this happen? Does longer max_length cause the model to generate meaningless
tokens?
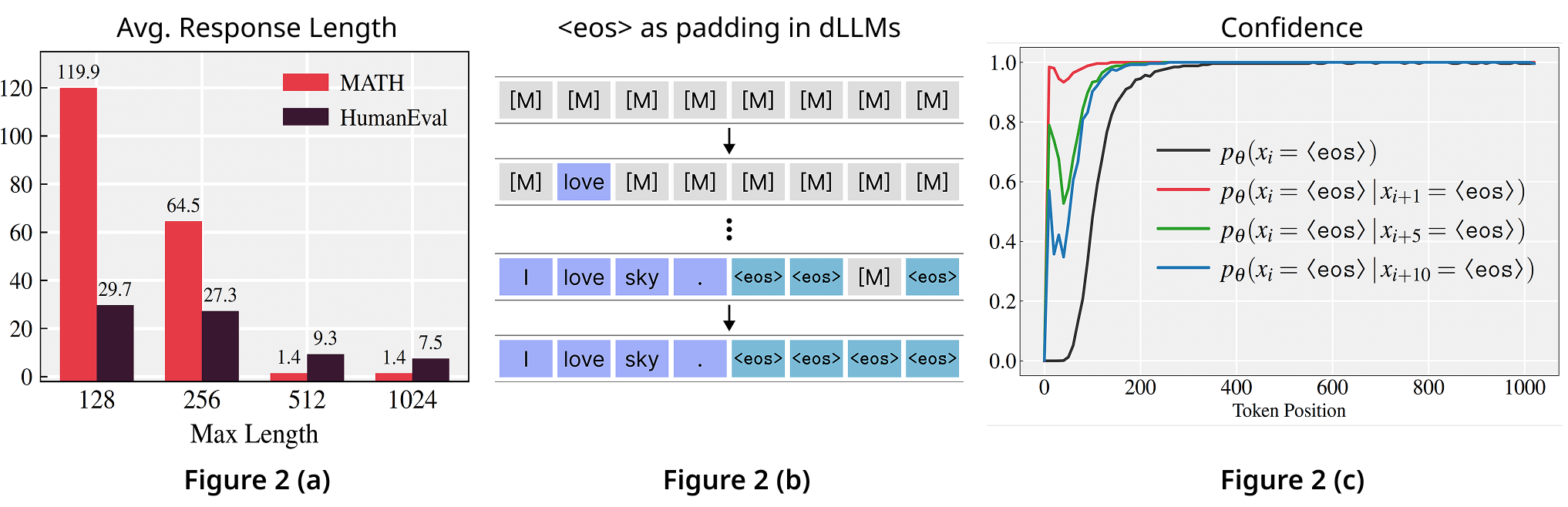
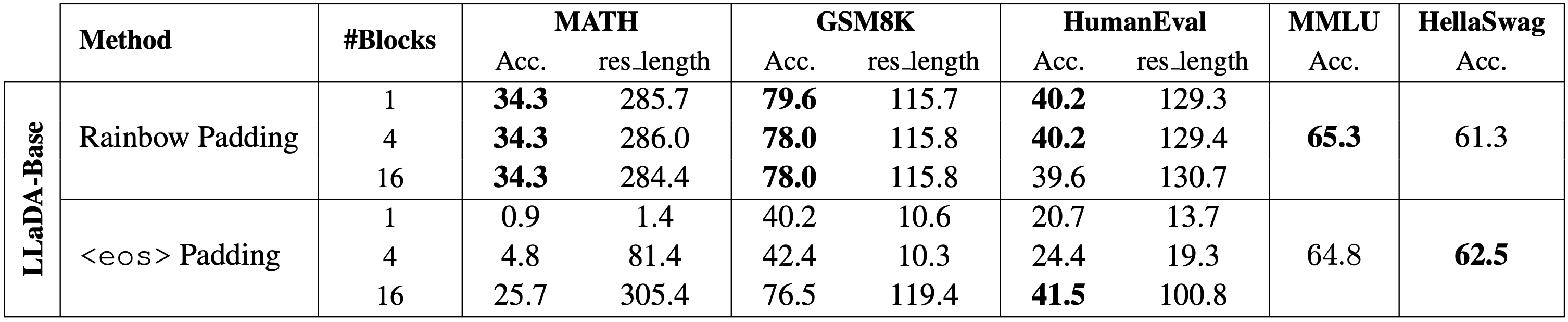
We found the opposite: models actually produce shorter responses as max_length
increases (Figure 2 (a)).
The root cause is using <eos> tokens for both termination and padding during
instruction tuning.
Figure 2 (b) shows how current dLLMs pad shorter sequences with <eos> tokens in
training.
This causes the model to learn inflated <eos> probabilities at later positions.
Figure 2 (c) reveals the cascade effect: <eos> confidence approaches 1.0 after ~400
tokens.
Under adaptive decoding strategies (confidence, margin, entropy), these high probabilities trigger early
<eos> sampling at later positions, which then biases earlier positions (even 10+ tokens
back) toward <eos> as well.
This creates a feedback loop: inflated <eos> probabilities → adaptive sampling
selects <eos> early → backward propagation → premature termination.
We call this phenomenon <eos> overflow.